Thursday, March 29, 2012
Missing person - HeatherLEGOGirl
If you're a regular reader of the variety of major LEGO blogs out there, you've already seen this, but I'm passing it along on the theory that at least some of my readers come from outside the hobbyist community. Heather Braaten, who you may know on various online forums as HeatherLEGOGirl, has been missing for the past week. She was last seen in Seattle, Washington. If you see Heather, or know anything of her whereabouts, please contact Lino Martins at linotopia AT hotmail DOT com , as he is in close touch with Heather's family, or directly contact the Seattle police department. Or use any of the contact information on the flyer below.


Wednesday, March 28, 2012
Monday, March 26, 2012
Sunday, March 25, 2012
The last Space Shuttle launch
I previously noted two Canadian teens who sent a minifig into near space using a weather balloon. Well, a few months ago, Romanian teen Raul Oaidia did much the same thing, sending a LEGO Space Shuttle into the stratosphere.
Saturday, March 24, 2012
Dem bones
Apparently making artificial bone is an extremely tedious process, but LEGO can help. Cambridge PhD candidate Daniel Strange, working in the laboratories of Michelle Oyen, has been working on ways to make bone, both for medical applications, but also for potential other materials use. The process involves repeated dipping of an object into various solutions and then rinsing. Daniel wanted to automate this process, but buying a commercial robotics system would be extremely expensive. So he built his own, using Technic pieces and a NXT system to control the whole thing. Be sure to watch the video so you can see it in action.


Friday, March 23, 2012
Orrery
One more from Aklego, but this time in astronomy rather than math. He made this great orrery. As I've previously described, an orrery is a machine to show the relative motions of the planets and moons.
Thursday, March 22, 2012
Hyperboloid
Aklego's hyperboloid is another great mathematical kinetic sculpture. A hyperboloid of one sheet is a three dimensional surface defined by the equation (x2/a2)+(y2/b2)-(z2/c2)=1. It essentially looks like a cylinder that's been squeezed in around the waist (I show an image below the video). This is another doubly ruled surface - that is, even though the surface is curved, it is made up of intersecting straight lines (the strings in the picture below). Aklego's video shows how this surface is defined by a straight line sweeping in a circular motion.


Wednesday, March 21, 2012
Hyperbolic parabaloid
Aklego also made this hyperbolic parabaloid. This is a saddle shaped three dimensional surface defined by the equation (z/c)=(y2/b2)-(x2/a2). This is an example of a double ruled surface. That is, each point on the surface is the intersection of two straight lines that are on the surface.
Tuesday, March 20, 2012
Trammel of Archimedes
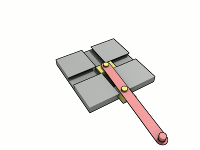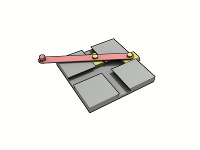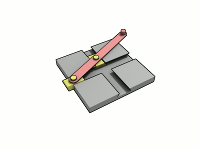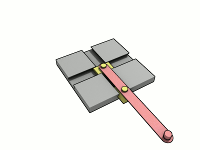
Wow, I just can't get away from this guy. I went on Brickshelf (a LEGO image sharing site), and one of the most recent postings was Gregvader's ellipsograph. An ellipsograph is also called a 'trammel of Archimedes', though it is unclear if these actually go back to Archimedes' day. Anyway, as two sliders go back and forth in their tracks, a pen on the swing arm draws out an ellipse. I've included a couple of animated gifs from Wikipedia so you can see this in action. The Wiki description notes that there is a children's toy called a "Do Nothing Machine" that is basically the same idea, and that reminds me that a LEGO version is described in the Klutz Book of LEGO Crazy Action Contraptions. I've included a version by BentWright and you can see a video showing it in action.







Monday, March 19, 2012
One last Archimedes
Okay, one last from Archimedes. He also designed the Archimedes screw, a screw blade inside a cylinder. When the screw is rotated, liquids or powders are lifted up from a lower tank into a higher position - e.g. to pump bilge water out of the hull of a ship, or to pump water into a canal. This principle was used a few different Great Ball Contraption (GBC) modules. The GBC is a collaborative Rube Goldberg contraption to move a bunch of LEGO balls around a loop. Each module accepts a load of balls and delivers it to the next. Look on YouTube to see fascinating videos of these in action. Anyway, here is a module by svbrckm and another by akiyuky.


Sunday, March 18, 2012
Eureka!
Following up on Archimedes from the other day (Pi Day), he is probably most famous for a story involving a bath. As the story goes, he was pondering how to measure the volume of an irregular object and he went to take a bath to relax. When he stepped into the full tub, some water spilled out over the edge. He realized that the amount of water displaced by a submerged object (him, in this case) was equal to the volume of the object. He yelled "Eureka!" (I found it!) and ran from the bath to tell others of his discovery, without even pausing to put on some clothes. Whether or not there is any truth to the story, his method is still used today. I've taught introductory labs in which we determine the density of a metal object by weighing it and then seeing how much water it displaces. The mass divided by volume is the density (along the way, this introductory lab teaches students to use the balance and the graduated cylinder). The perhaps apocryphal bathtub story has been recreated in LEGO form by Spiderpudel, Superdave42 and Lord Pappadhum. (Hmm, two of these were built for the Reasonably Clever Mad Scientist Contest. I've featured a couple of those creations here before, but I have to remember to go back and feature others. It's particularly embarrassing that I haven't already done so, since I was one of the judges for that contest.)






Squaring the circle
One more from Cole Blaq's fun Enter the Brick series: Circling the Square. This name refers to the old challenge of squaring the circle. The challenge was to use a compass (the kind you use to draw circles, not the kind you use to find your way in a forest) and a straight edge to draw a square with the same area as a given circle. The 1882 proof that this is impossible was also very important for number theory, as it helped show the transcendental irrational nature of pi.


Saturday, March 17, 2012
Squaring the circle
One more from Cole Blaq's fun Enter the Brick series: Circling the Square. This name refers to the old challenge of squaring the circle. The challenge was to use a compass (the kind you use to draw circles, not the kind you use to find your way in a forest) and a straight edge to draw a square with the same area as a given circle. The 1882 proof that this is impossible was also very important for number theory, as it helped show the transcendental irrational nature of pi.


Friday, March 16, 2012
Melting point
While digging through Cole Blaq's photostream to find an appropriate spray can model for my previous blog post, I once again enjoyed looking at his Enter the Brick series of sculptures based on the basic LEGO brick. One that deserves some highlight here is his melting point. The melting point is the temperature at which a solid changes into a liquid form. When I'm teaching about melting point, I often use LEGO bricks as an analogy (or just basic brick walls). A solid crystal is like a wall built of overlapping LEGO bricks. Each molecule is interacting with the molecules around it via a series of forces. As temperature is added, these molecules vibrate more and more. At some point, the force of the molecules vibrating is greater than the force holding them together, and so they start to slide past each other--i.e. go from the solid phase to the liquid phase. In a pure sample, each 'brick' is in a completely identical situation, and so each 'brick' is held to its neighbors by identical forces. Because of this, it takes the exact same amount of heat energy to break apart each of the bricks, and so there is a sharp melting point (that is, everything melts within a couple of degree range). On the other hand, if you have a mixture of different types of bricks, they don't fit together as neatly or as regularly. Therefore it takes less heat energy to cause melting (this is why, btw, you dump salt on the ice on your sidewalk), and, since each brick is in a slightly different situation and is therefore held to its neighbors by a different amount of force, the melting happens over a much broader range.


Thursday, March 15, 2012
F. Sherwood Rowland and CFCs
A few days ago F. Sherwood Rowland, a retired professor of chemistry from UC Irvine, passed away at the age of 84. Professor Rowland is best known for being awarded the 1995 Nobel Prize in Chemistry for his work on chlorofluorocarbons. These compounds, known as CFCs, had a number of uses, such as refrigerants in cooling systems and propellants in aerosol spay cans. Rowland and his colleagues realized that CFCs were long-lived compounds that would remain in the environment, and they were light enough that they would find their way into the upper reaches of the atmosphere. There they would be bombarded by UV light (wavelengths of light that largely don't reach us down here at the earth's surface as they are absorbed by the ozone layer) which would cause them to break down. The product of this breakdown would be free radicals. That's a term you've probably heard of in terms of health issues - that free radicals cause damage to the body and that antioxidants (e.g. certain compounds in blueberries) can help counteract the effects. The reason free radicals cause damage is that they include unstable atoms that need one electron to become more stable. They will get this electron from whatever molecule they run into. If this is in your cells, a hydroxyl radical can run into your DNA or your proteins, and lead to damage to these important biomolecules. If this is in the upper atmosphere, chlorine radicals can run into ozone (O3) molecules and cause them to break down into the more common O2 molecules. The significance is that a drop in the concentration of ozone in the upper atmosphere lets more harmful UV light through to those of us down here at the earth's surface. In response to the work of Rowland and his colleagues, the Montreal Protocol in 1987 started to phase out the production of CFCs worldwide in order for the ozone layer to recover.

LEGO builder Cole Blaq has made a whole series of spay can models that are really fascinating. Decode is one of his most recent. I thought it was particularly nice for this blog, since in addition to relating to spray cans, there are also themes of DNA and robotics.

LEGO builder Cole Blaq has made a whole series of spay can models that are really fascinating. Decode is one of his most recent. I thought it was particularly nice for this blog, since in addition to relating to spray cans, there are also themes of DNA and robotics.
Wednesday, March 14, 2012
Happy Pi Day
Today, March 14, or 3/14, is Pi Day (hmm, Europeans tend to put the day before the month, so I wonder if they do this on April 31 - oops, there is no April 31). Anyway, lift a glass at 1:59 (and 26 seconds, if you're really precise) to Archimedes, who approximated pi in the third century BC. In celebration, here are some LEGO circles. Well, to be precise, these aren't really circles, but instead are polygons with very large numbers of sides, but Flatland taught us that once you got enough sides it was pretty tough to tell the true circles from the high-order polygons. BTW, making circles out of square bricks has been a challenge for LEGO builders, and get incorporated into all kinds of great creations like castles and spaceships.
















Monday, March 12, 2012
Lewis structures
Chris Masi is a professor of chemistry at Westfield State University and also an LEGO builder and member of NELUG. He brought his profession and his hobby together in an exercise to teach Lewis structure using LEGO bricks. He presented this project at an education symposium at the 2008 meeting of the NorthEast Regional Meeting of the American Chemical Society.


Friday, March 9, 2012
Anesthesia Delivery Unit
Professional LEGO builder Eric Harshberger made this amazing full-scale replica of an anesthesia delivery unity. This was used by GE Healthcare as a booth exhibit at a trade show.

Here it is next to the real thing.
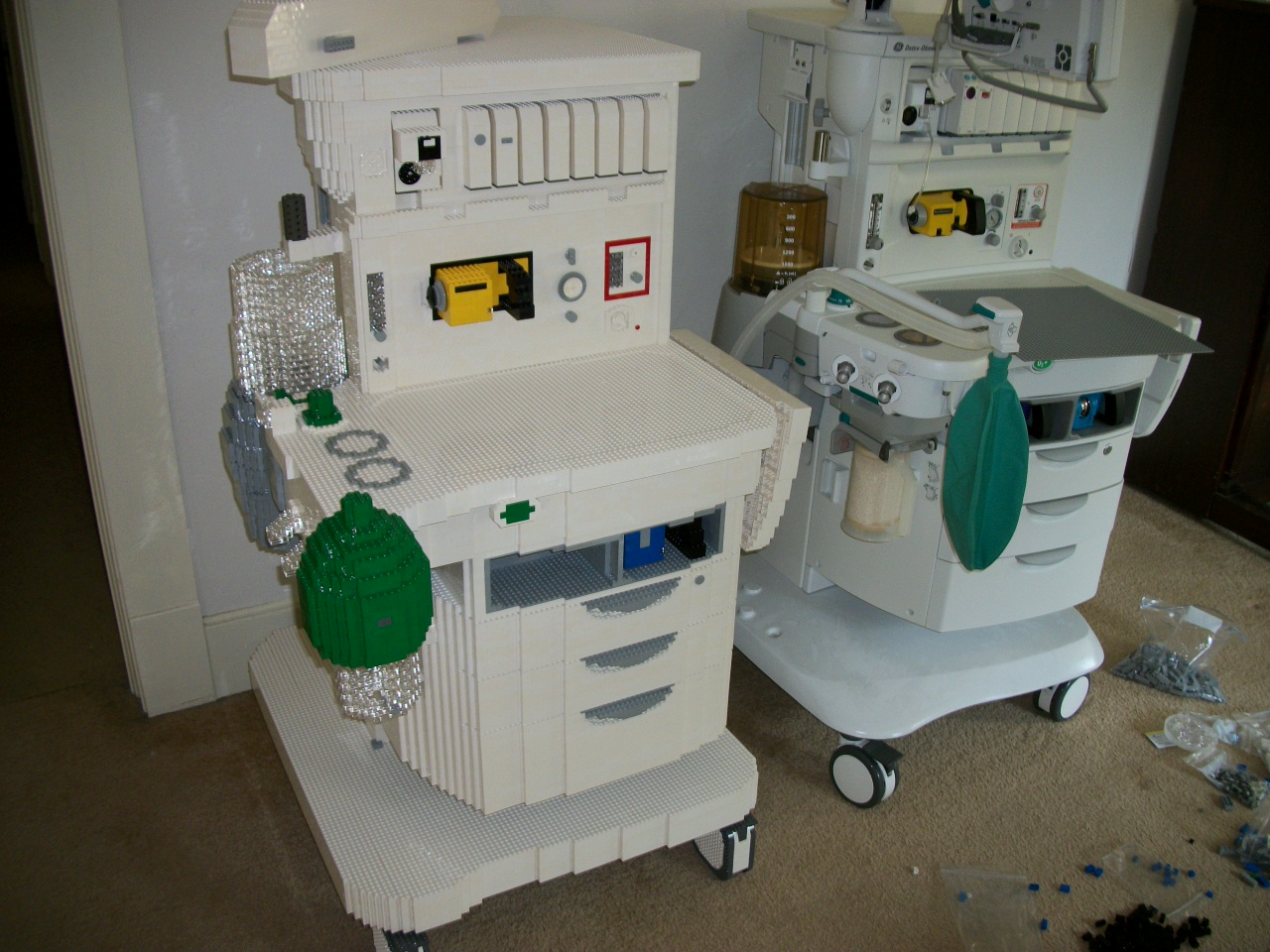

Here it is next to the real thing.

Thursday, March 8, 2012
Lewis structure
A Lewis structure is a representation of atoms and electrons that show how a molecule is constructed. Atoms reach their most stable state when they are surrounded by eight valence electrons (the "octet rule"). These electrons might be lone pairs--two electrons that are just associated with that atom--or covalent bonds--two electrons that are shared between two atoms. When there is a covalent bond, both atoms count the shared electrons as part of their 'valence spheres'. In a Lewis structure, lone pairs are represented by pairs of dots, while covalent bonds are represented by straight lines connecting two atoms. It looks like Lego27bricks is taking introductory chemistry, since his LEGO self is trying to figure out a Lewis structure.


Thursday, March 1, 2012
Fermat's last minifig
Pierre de Fermat (here LEGO-ized by Michael Jasper) was an important mathematician, a contemporary of Descartes and an inspirer of Newton. He's probably most famous for his "last theorem". We all know that for a right triangle, the side lengths work out so that a2+b2=c2. There don't seem to be any integers that fit into equations such as a3+b3=c3 or a4+b4=c4. Fermat noted in the margin of a book he was reading that he had a proof for that, and for all other integer powers greater than 2, but he didn't have space to write down his proof. This inspired the next two centuries of mathematicians, until Andrew Wiles finally completed the proof in 1995. He received a knighthood for his work! Who says mathematicians aren't cool?


Subscribe to:
Comments (Atom)