Impossible objects explained

I occasionally draw something like this on the board and ask my students what it is:

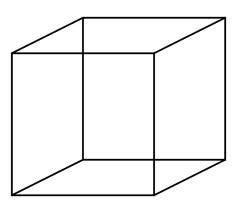
When they reply 'a cube' I correct them, saying that it is a two dimensional drawing that uses tricks of perspective that our mind interprets as a three dimensional cube. Two dimensional drawings of impossible objects take advantage of these tricks of perspective, but the tricks don't match up. So if you cover up one part of the drawing and then cover up the other part of the drawing, different sections appear to be going in different directions. For example, take the famous devil's fork:

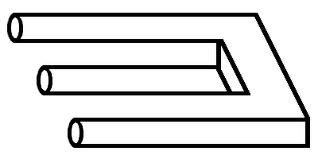
If you cover up the right-hand portion, you see three prongs, but if you cover the left portion you see two prongs. However, the lines connect up so at some point the three become two, or the foreground becomes the background. But how to achieve this in three dimensions? The whole idea of an impossible object is that it is impossible. The answer, of course, is that you can only see these from one particular point of view. If you were to look at them from any other angle, you would see that the edges don't match up. For instance ...

Brixe63's Terrace.



Legohaulic's Nightmare.



Henry Lim's Ascending and Descending.



Andrew Lipson and Daniel Shiu's Belvedere.